初等量子力学講義録2005年第12回



←第11回へ　初等量子力学・量子力学(2005年)の目次に戻る　第13回へ→

　前回飛ばしてしまった波動関数の規格化の話から。
　以上のように、波動関数の絶対値の自乗ψ*ψがその場所に粒子がやってくる確率に比例するだろうと考えられる。「比例」ではなく厳密に「確率密度」にするためには、
∫

考えている全空間 
 dx ψ* ψ = 1
(7.18)
となるようにしておけばよい。このようにすることを規格化(normalization)と言う。具体的には、もし
∫

考えている全空間 
 dx ψ* ψ = N
(7.19)
となったならば、
ψ新 = 1
√N
 ψ
(7.20)
として新しいψ新を作ればよい。



下のグラフで表されるような波動関数がある(実数部分だけで虚数部分はない)。
△波
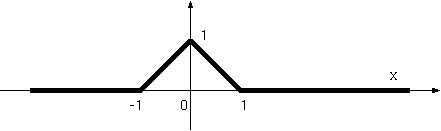[問い7-1] 規格化せよ。
[問い7-2] 確率密度ψ*ψのグラフの概形を書け。
[問い7-3] a < x < a+1の範囲で粒子が発見できる確率を、aの値によって分類して表にせよ。



7.3  なぜ波動関数ψは複素数なのか？

　シュレーディンガー方程式の波動関数は、複素数であることが不可欠である。その理由を知るために、話を少し古典力学に戻す。
古典的なニュートン力学で、粒子の運動をどのように解いていたかを思い出そう。「運動を解く」とは、任意の時間における粒子の座標→x(t)を求めることである。
　ニュートン力学の中心となる方程式は運動方程式
m
d2 →
x
 
 (t)
dt2
 = →
f
 
(7.21)
である。→xの２階微分がこの式によって決定されるので、この式を２回積分すれば、それより未来の全ての時間での→x(t)を計算することができる。そのためには初期値としてある時刻での→x(t)と[(d→x(t))/dt] を与える必要がある。
古典力学のニュートン方程式は２階微分の方程式であるがゆえに、一つの座標x(t)に対して二つの初期条件が必要になった。古典力学でも、正準方程式は


dpi(t)
dt
=− ∂H
∂xi
 ,       dxi(t)
dt
 = ∂H
∂pi

(7.22)
という１階微分方程式である。しかしこの場合は力学変数が座標と運動量の二つに増えていて、初期値はやはり、→x(t),→p(t)の二つについて与える必要がある。
一方、量子力学では運動量→pがド・ブロイの式によって波長λと関係付けられている。そしてこの波長というのは、ある瞬間の波の形から決まるものであるから、量子力学における運動量は、ある瞬間で定義されているものである。これは古典力学との大きな違いである。多くの場合、古典力学の運動量は

→
p
 
 (t)=mv(t)=
lim
∆t→0 
m( →
x
 
 (t+∆t)− →
x
 
 (t))
∆t
(7.23)
と表される。→p(t)は∆tという(短い)時間間隔の間での引き算で定義されている。



力学変数 基本方程式 初期条件
古典力学
(ニュートン)		xi(t) m [( d2 xi)/dt]=fi xi(t=0),[(dxi)/dt](t=0)
古典力学
(ハミルトン)
xi(t),pi(t)
dx
dt
= -
∂H
∂xi		 ,    
dpi
dt		 =
 ∂H
∂pi
xi(t=0),pi(t=0)
量子力学 ψ(→x,t)
ihbar=
 ∂ψ
∂t		= H ψ 
ψ(→x, t=0)


　シュレーディンガー方程式は１階微分方程式なので、ψ(→x,t)の中には、→x,→pに対応する量が両方入っていなくてはいけない。
さて、ではψが複素数でなくてはならない理由を説明しよう。ψを実数で表すことができたとする。簡単のため１次元問題で考えると、xの正方向へ進行する波は
Asin( 2π( x
λ
 −νt) +α)
(7.24)
のように書けるだろう。逆方b向へ進行する波の式は、上の式でx→ −xという置き換えをやればよいので、
Bsin( 2π( − x
λ
 −νt) +β)
(7.25)
と書けるだろう。
　ところがこの二つ、(7.24)と(7.25)は、t=0にしてしまうとどちらも
Asin( 2π x
λ
 +α) と  Bsin( −2π x
λ
 +β)
(7.26)
となって区別がなくなってしまう。一見して違うように見えるかもしれないが、任意定数であるA,B,α,βを適当に選ぶとこの二つは同じものになる（たとえばB=−Aとしてα = -β(マイナス符号忘れてました)にしてもよいし、A=Bにしてα = β+πとしてもよい）。
　つまり、実数の波で考えると、初期状態の中に波の進行方向という情報が入らなくなってしまうのである。複素数であれば、
Ae2πi([x/λ]−νt)+α     と      Be2πi(−[x/λ]−νt)+β
(7.27)
はt=0にしても、
Ae2πi[x/λ]+α     および      Be−2πi[x/λ]+β
(7.28)
というふうに違いが出る。つまり、初期値(t=0での瞬間の値)の中に「運動量の向き」という情報が含まれるようにするためには、複素数であることが必要なのである。
虚数波と実数波の進行
　e−2πiνtという形の式になっているので、ある一点に着目する と、波の位相は常に減少していく。よって上の図のように実部と虚部が変化する(たとえば実部が最大値(プラス)を迎えた後、虚部が最小値(マイナス)を迎 える)ためには、波がどっち向きに動かなくてはいけないか、と考えれば波の進む向きがわかる。
　ここで、 Ae2πi( ±[x/λ]x+νt )のような形の波は考えなかったが、これはマイナスのエネルギーを持っていることに対応するので、物理的には出てこない。
　電気回路の問題で交流を考える時にもI0cosωt→ I0 eiωtと拡張して電流を複素数化して計算することがあったが、あれはあくまで計算の便法であり、付け加えられた虚数部iI0sinωtには物理的意味はない。しかし量子力学での波動関数の虚数部は、立派な物理的意味がある。
　なお、正確には、波の方向を表すものが波動関数の中に入ってくるようになってさえいれば、波 動関数が複素数である必要はない。しかし、実数１成分の場では波の方向を表すものは作れない。たとえば電磁波は実数の波であるが、常に電場と磁場という二 つの場がセットになって出てきており、波の進む方向は→E×→Hの方向として求めることができる。電磁波のうちある一瞬の電場部分だけ(あるいはある一瞬の磁場部分だけ)を見たのでは波の進む方向はわからない。電場と磁場の両方を見ると、「電場→磁場」と右ネジを回した時にネジの進む向きが電磁波の方向であるとわかる。
　つまり波の進行を表すためには、複素数というよりは実数２成分の自由度が必要なのである。波動関数も、複素数で書くのがどうしても嫌なら、実数２成分の関数を使って表すこともできる。ただしその場合、運動量は行列で表されることになって計算がややこしくなる。



[問い7-4] １次元の波動関数を、ψ(x,t)=ψR(x,t)+iψI(x,t)とおく。ψR,ψIは各々実数関数である。このように分けて書いた時、シュレーディンガー方程式の実数部分と虚数部分はそれぞれどのような方程式になるか。



7.4  演習問題

[演習問題7-1] 波動関数ψ(→x,t)がψ(→x,t)=φ(→x)e−[i/hbar]Etと書ける時、φ(→x)が満たすべき方程式を求めよ。この方程式は「定常状態のシュレーディンガー方程式」と呼ばれる。
[演習問題7-2] 波動関数ψ(→x,t)がψ(→x,t)=φ(→x)e−[i/hbar]Etと書ける時は、ψ*ψが時間によらないことを示せ。また、エネルギーの原点をずらしてもψ*ψには影響がないことを確かめよ。
[演習問題7-3] 以下のような関数で表される波動関数を考える(考える範囲は [−π,π]としよう)。それぞれを規格化し、確率密度のグラフの概形を書け。

  1. ψ(x)=sin(x)

  2. ψ(x)=einx (nは整数)


  3. ψ(x)
    =
    x     ( for  x ≥ 0)


    ψ(x)
    =
    −x   ( for  x < 0)
[演習問題7-4] 質量mを持つ自由粒子の波動関数がψ(x,t)=sinx f(t)で表されるとする。シュレーディンガー方程式を解いてf(t)を求めよ。
結果としてできあがるψ(x,t)は、右へ進行する波と左へ進行する波の重ね合わせであることを示せ。
[演習問題7-5] 質量mの物体が長さLの棒につながれ、原点に固定された棒のもう一方の端を中心に回転しているとする。この時のラグランジュアンはL=1/2mL2 ([dθ/dt])2、ハミルトニアンは[1/(2 mL2)](pθ)2である。波動関数をψ(θ)として、この系に対する定常状態のシュレーディンガー方程式を作って解き、エネルギーの値を求めよ。θ = 0とθ = 2πで波動関数の値が同じにならなくてはいけないことに注意せよ。
[演習問題7-6] ある面(x=0)を境界として上(x > 0)ではポテンシャルがV（定数）、下(x < 0)ではポテンシャルが0になっているとする。つまり、上では

[ − hbar2
2m
∂2
∂x2
 +V] ψ = ihbar ∂
∂t
 ψ
が、下では
− hbar2
2m
∂2
∂x2
 ψ = ihbar ∂
∂t
 ψ
が成立する。解の形をψ = Aei(kx−ωt)と仮定して方程式を解け。両方で振動数が等しい（エネルギーが保存する）場合を考えると、上から下へ入射した時、波長はどのように変化するか。
[演習問題7-7] 平面波解ψ = Aei(kx−ωt)においては、ψ*ψが場所によらないことを示せ。なぜこのようになるのかを、不確定性関係から説明せよ。
[演習問題7-8] ３次元の自由粒子のシュレーディンガー方程式は
− hbar2
2m
( ∂2
∂x2
 + ∂2
∂y2
 + ∂2
∂z2
) ψ = ihbar ∂
∂t
 ψ
である。この式の解をψ = Aei(kx x+ky y + kz z −ωt)とした時、ωをkx,ky,kzで表せ。
[演習問題7-9] １次元の自由粒子のシュレーディンガー方程式
− hbar2
2m
∂2
∂x2
 ψ = ihbar ∂
∂t
 ψ
にガリレイ変換(x′=x−vt,t′=t)を施し、ψの満たすべき(x′,t′を変数とした)方程式を作れ。この式は、元々の座標系から見て速度vで運動しているような座標系での方程式である。
こうすると式の形が変わってしまうが、ここで波動関数を
ψ = ei(kx+εt)Ψ
とおき、k,εを適当に選べば、Ψの満たす方程式は元のシュレーディンガー方程式と全く同じ形になる。k,εを求めよ。

第8章　波束の進行

8.1  波の群速度と位相速度

波の重なりでできる波の塊 
　一般の波はいろんな波長を持った波が重なったものと考えることができる。そして、波の重なりによってできた「波の塊」が我々が粒子として感知するものであ ろうと考えられる。この「波の塊」を波束(wave packet) と呼ぶ。波動関数が一個の粒子の存在確率を表すとすれば、波がうまく重なりあって強め合っていて、結果として粒子の存在確率が高くなっている場所が粒子が 一番いそうな場所である。右の図はいくつかの異なる波長の波が重なりあった状態を示しているが、足し算された波の位相がきれいにそろっている中央の場所が もっとも高い山となっている。ではこの後波が進行していくと、この場所はどのように動くだろうか。
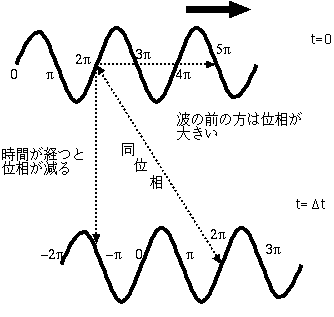位相速度の図
　まず、単色波（１種類の波長の波しか入っていない場合）について考えよう。今、波数(定義は[2π/波長])がkで、角振動数(2π×振動数で定義される)がωであり、x軸正方向に進行している波を考えると、その波はeikx−iωtのような式で表すことができる。この波の速度はvp = [k/ω]である。この式の形から、時間が∆t増加すると位相がω∆t減少すること、x軸正方向に∆x移動すると位相がk ∆x増加することがわかる。波の同位相の点は、k∆x = ω∆tを満たす場所に移動する。つまり、[∆x/∆t] = [ω/k](テキストは分母分子逆でした）である。
この速度vp=[ω/k]はeikx−iωtで表される波の、同位相の点がどのように動いていくかを示す速度なので「位相速度」(phase velocity)と呼ぶ。そしてこれは「波束(あるいは「粒子」)の動く速度」とは一致しない。そもそも、eikx−iωtという波は、宇宙の端から端まで(x=−∞からx=∞まで)常に同じ振幅1で振動している波であって、波の「塊」になっていない。つまり波束を作るには単色波ではだめで、いろんな波長の波(いろんなkの波)を足し合わせて「塊」を作らなくてはいけない。
　次に単色波ではない簡単な例として、２種類の波長の波の和を考えよう。波数k−∆kで角振動数ω−∆ωの波と波数k+∆kで角振動数ω+∆ωの二つの波を重ねてみる。この二つの波を同じ振幅として足すと、

ei((k−∆k)x−(ω−∆ω) t) + ei((k+∆k)x−(ω+∆ω) t) =
ei(kx−ωt)(e−i(∆k x− ∆ωt)+ei(∆k x− ∆ωt))
=
2ei(kx−ωt)cos(∆k x− ∆ωt)
(8.1)
となる。この結果は二つの波2ei(kx−ωt)とcos(∆k x− ∆ωt)のかけ算である。
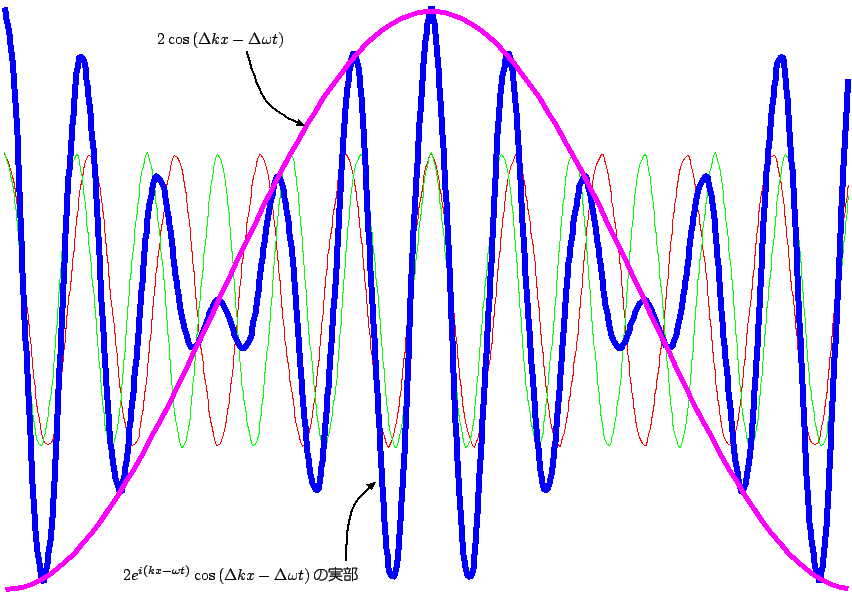
二つの波の重なりあい
　この波の実数部分をグラフ化して示したのが上の図である。

　グラフもいいが、例によってjavaアプレットで動くものが作ってあるので、そっちを見て欲しい。

この波はいわば、平面波ei(kx−ωt)の振幅が2cos( ∆k x− ∆ωt ) に応じて変化していると考えることもできる。そしてこの振幅の変化は[π/∆k]の幅の「波のこぶ」を作る。そのこぶは[∆ω/∆k]という速度で進行していくことになる。
もう少し一般的に、二つ以上のたくさんの波が重なって波束を作っている場合を考えよう。ある波の塊が

∫ dk f(k)eikx − iω(k)t
(8.2)
のように、いろんなkを持つ波の和で書かれて いるとしよう。f(k)は、いろんなkの波をどの程度の重みをもって足し算していくかを表す関数である。ここで、ωをω(k)と書いてkの関数であるとし た。ω とk にはなんらかの関係があるのが普通である(「分散関係」と呼ぶ)。
この波がk=k0を中心としたせまい範囲でだけf(k) ≠ 0であるような波だとする。そのような時は
ω(k)=ω(k0)+ dω
dk
 (k−k0) + …
(8.3)
と展開して、…で示した(k−k0)2のオーダーの項は無視できる。それを(8.2)に代入すると、
eik0 x − iω(k0)t


∫ dk f(k)ei(k−k0)x − i[dω/dk](k−k0)t
x−[dω/dk]tの関数 
(8.4)
となる。この後ろの部分はx−[dω/dk]tの関数になっているので、これをF(x−[dω/dk]t)と書くと波は
eik0 x − iω(k0)t F(x− dω
dk
 t)
(8.5)
と書ける。 さっきやった二つの波の足し算の式で言うと、2cos( ∆k x− ∆ωt ) に対応する部分がF(x−[dω/dk]t)である。
つまり、今考えた重ね合わされた波は、場所によって違う振幅（F(x−[dω/dk]t)）を持っている、eik0 x − iω(k0)tで表される波であると近似して考えることができる。
この振幅の部分はF(x)という関数をx方向に[dω(k)/dk]tだけ平行移動させたもの、と考えることができる。ゆえに、この振幅は
vg = dω(k)
dk
(8.6)
という速度をもって移動していることになる。この速度vgを波の塊（グループ）の速度という意味で、群速度(group velocity)と呼ぶ。
古典力学と量子力学の対応を考えた時に、「波動関数の位相が極値を取るときが古典的運動であ る」と考えたが、群速度を考える時も同様にして考えることができる。波の位相がϕ = kx − ω(k) tだとする。群速度というのは「波の振幅が大きくなっている部分」の進行速度であるが、振幅が大きくなるためには、その波束を構成している一個一個の波eiϕの位相がそろっていればよい。よって位相ϕをkで微分して0になる点では「位相変化が０になって、波が強め合っている点」だと考えることができる。この条件から、群速度を求めても同じ結果が出る。
　自由なド・ブロイ波の場合、k=[2π/λ]でhbarω = [(h2)/(2mλ2)]であるから、ω(k) = [(hbar k2)/2m]となり、位相速度は
vp =
hbark2
2mλ2
2π
λ
 = h
2mλ
 = hbark
2m
(8.7)
であり、群速度は
vg = d
dk
( hbark2
2m
) = hbark
m
 = h
mλ
(8.8)
である。つまり、vg = 2vpである。この式からmvg = [h/λ]が成立していることがわかる。つまり、波束を粒子と見た時の運動量mvgが[h/λ]に対応する。このように波の伝わる速度には２種類あるが、古典力学での粒子の運動と対応しているのは群速度の方である。

　波動関数の群速度は、古典的運動の速度という意味があるが、では位相速度はというと、実は波動関数の位相速度はほぼ、観測にかからない。我々が粒子を観測するときは、あくまで波束の運動として捉えるので。

　いつでも位相速度の方が遅いんですか？
　いえ、逆の場合もあります。特別な状況の電磁波なんかでは、位相速度の方が速くなって、光速を超えたりするけど、それは心配ありません。

　投げ上げ運動を量子力学的に考えると上に行くほど波長がのびることによる屈折であると考えることができた。この時、波長が伸びると位相速度vp=λνは速くなる。しかし、群速度の方は古典的な速度と同様、遅くなっていく。

8.4  演習問題（今回の内容に関係ある問のみ）

[演習問題8-1] [演習問題7.4]の場合、位相速度と群速度はx > 0とx < 0で、それぞれどのような変化をするか。
[演習問題8-2] 相対論的粒子の場合、エネルギーと運動量の関係はE=√[(p2c2+m2c4)]である。E=(h/2p)ω, p=(h/2p) kはこの場合でも成立するので、ωとkの関係は (h/2p)ω = √{(h/2p)2k2c2+m2c4} である。この場合の位相速度vpと群速度vgを波数kの関数として求め、vpvg=c2であることを確認せよ。vpとvgのうち一方は光速を超えることになるが、それはどちらか。これは物理的に許される結果だろうか？

学生の感想・コメントから

　位相速度が光速超える例はありますか。
　導波管内の電磁波とかです。

　位相速度が光速超えてもいいんですか。
　かまいません。何か（エネルギーとか情報とか）を運ぶ速度ではないからです。

　波の実数部だけでグラフ書いてましたが、虚数部も入れるとどうなるんでしょうか？
　位相がπ/２だけ小さい波が重なります。グラフに描くとごちゃごちゃしすぎて見にくくなるかも。

　そろそろテスト勉強をしなくちゃ、と思った（複数）
　「そろそろ」じゃだめ！
　どんな学問もそうだけど、量子力学のような、世界を捉える概念自体をひっくり返さなきゃいけないような学問は特に、日々の積み重ねが物を言う。概念をひっくり返すということは簡単にはできません。テストの前にだけ勉強するようでは量子力学には太刀打ちできない。

　投げ上げ運動しているときは位相速度が増加し群速度が減少するそうですが。目の前を飛んでいうホコリは上がったり下がったりしているように見えるのですが、この場合も同様のことが起こっているんでしょうか。
　上に移動する→位置エネルギー減少→波長伸びる→位相速度増加と同時に群速度減少
およびこの逆が、上下運動するたびに起こってます。

　海の波にも位相速度と群速度はあるんでしょうか？
　波が波束状態になっている時には位相速度と群速度が定義できます。

　位相速度が観測できないとすると、どうやって「群速度より速い」とわかるんでしょうか？
　そういう意味では、わかりませんね。今日やった計算の場合は、シュレーディンガー方程式や波動関 数の形をある程度仮定して、位相速度や群速度を計算で求めているわけです。仮定が違ったら位相速度が違ってしまうことはあります。群速度の方は観測できる 量なので、正しい仮定を採用して計算している限り変わりません。　

　テストってどの辺出るんですか？
　全部。

File translated from TEX by TTHgold, version 3.63.
On 8 Jul 2005, 12:18.