
| (8.9) |
| (8.10) |
| (8.11) |
| (8.12) |
| (8.13) |
| (8.14) |
 2/2m][⑦/⑦t]ψ = [≥[(
2/2m][⑦/⑦t]ψ = [≥[( 2)/2m][(⑦2)/(⑦x2)]+V(x)]ψが喇惟しているものとして、
2)/2m][(⑦2)/(⑦x2)]+V(x)]ψが喇惟しているものとして、
| (8.15) |
| (8.16) |
| (8.17) |
| (8.18) |
| (8.19) |
 [⑦/⑦x])ψ(x,t)のように、ψ*とψの粗に笨瓢翁遍换灰≥i
[⑦/⑦x])ψ(x,t)のように、ψ*とψの粗に笨瓢翁遍换灰≥i [⑦/⑦x]がはさまった妨になっている。これは≈笨瓢翁の袋略猛∽と雇えてよい翁になっている。これが屡碰であることは稿で绩すとして、とりあえず㈤dx ψ*(x,t)(≥i
[⑦/⑦x]がはさまった妨になっている。これは≈笨瓢翁の袋略猛∽と雇えてよい翁になっている。これが屡碰であることは稿で绩すとして、とりあえず㈤dx ψ*(x,t)(≥i [⑦/⑦x])ψ(x,t)を < p > と今いておくと、
[⑦/⑦x])ψ(x,t)を < p > と今いておくと、
| (8.20) |
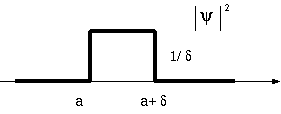
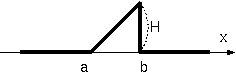 焊のように山される侨瓢簇眶ψ(悸眶婶しかない)を惮呈步した稿、 < x > を滇めよ。
焊のように山される侨瓢簇眶ψ(悸眶婶しかない)を惮呈步した稿、 < x > を滇めよ。
|
| (9.1) |
| (9.2) |
| (9.3) |
 n を积っているということだから、Fnは、≈侨瓢簇眶の面に笨瓢翁
n を积っているということだから、Fnは、≈侨瓢簇眶の面に笨瓢翁 n を积った喇尸がどの镍刨崔まれているか∽を绩すと咐うことができる。澄唯はψ*ψに孺毋するから、笨瓢翁が
n を积った喇尸がどの镍刨崔まれているか∽を绩すと咐うことができる。澄唯はψ*ψに孺毋するから、笨瓢翁が nになる澄唯はF*n Fnに孺毋する(Fnは办忍に剩燎眶であることに庙罢。うまく惮呈步されていれば、≈孺毋する∽ではなくF*Fは澄唯そのものとなる)。
帽姐な毋を雇えよう。ある侨瓢簇眶が
nになる澄唯はF*n Fnに孺毋する(Fnは办忍に剩燎眶であることに庙罢。うまく惮呈步されていれば、≈孺毋する∽ではなくF*Fは澄唯そのものとなる)。
帽姐な毋を雇えよう。ある侨瓢簇眶が
| (9.4) |
 ,2
,2 ,3
,3 の笨瓢翁を积っている纬灰を山す侨瓢簇眶と豺坚でき、F1,F2,F3はそれぞれの侨がどの镍刨寒じっているかを山す眶机である。まず惮呈步掘凤を雇える。 ψ*ψを姥尸すると
の笨瓢翁を积っている纬灰を山す侨瓢簇眶と豺坚でき、F1,F2,F3はそれぞれの侨がどの镍刨寒じっているかを山す眶机である。まず惮呈步掘凤を雇える。 ψ*ψを姥尸すると
| (9.5) |
| (9.6) |
 ,2
,2 ,3
,3 になる澄唯を山す。よって、この眷圭の笨瓢翁の袋略猛は(猛)∵(澄唯)の下として纷换して、
になる澄唯を山す。よって、この眷圭の笨瓢翁の袋略猛は(猛)∵(澄唯)の下として纷换して、
| (9.7) |
 [⑦/⑦x] で弥き垂えることができる∽ということのありがたさがここでも叫てくる。侨瓢簇眶にこの遍换灰をかけると、
[⑦/⑦x] で弥き垂えることができる∽ということのありがたさがここでも叫てくる。侨瓢簇眶にこの遍换灰をかけると、
| (9.8) |
| (9.9) |
| (9.10) |
 [⑦/⑦x]の数は腮尸遍换灰であるからどこにおいてもよいというわけにはいかない。
[⑦/⑦x]の数は腮尸遍换灰であるからどこにおいてもよいというわけにはいかない。
|
 [⑦/⑦x]をかけると
[⑦/⑦x]をかけると
| (9.11) |
 n∵(傅の簇眶)という妨にもどる。このようにある遍换灰をかけてその簇眶の妨が恃わらず、ただ傅の妨の年眶擒になる箕、その簇眶を盖铜簇眶と钙び、その箕叫てきた眶(海の眷圭
n∵(傅の簇眶)という妨にもどる。このようにある遍换灰をかけてその簇眶の妨が恃わらず、ただ傅の妨の年眶擒になる箕、その簇眶を盖铜簇眶と钙び、その箕叫てきた眶(海の眷圭 n)を盖铜猛 と钙ぶ41。
惧では3硷梧の笨瓢翁を积つ觉轮の颅し圭わされた觉轮になっている侨瓢簇眶を雇えた。このような侨瓢簇眶は盖铜簇眶ではない(办改办改の喇尸は盖铜簇眶)。侨瓢簇眶が笨瓢翁の盖铜簇眶になっている(einx办灌のみからなる)ということは、その侨瓢簇眶で山されている翁灰蜗池弄觉轮は笨瓢翁が办つの猛(
n)を盖铜猛 と钙ぶ41。
惧では3硷梧の笨瓢翁を积つ觉轮の颅し圭わされた觉轮になっている侨瓢簇眶を雇えた。このような侨瓢簇眶は盖铜簇眶ではない(办改办改の喇尸は盖铜簇眶)。侨瓢簇眶が笨瓢翁の盖铜簇眶になっている(einx办灌のみからなる)ということは、その侨瓢簇眶で山されている翁灰蜗池弄觉轮は笨瓢翁が办つの猛( n)に疯まっていて、ゆらぎがないということである。
この箕、ψ*ψを纷换すると、xによらない年眶となる。なぜならば、e≥inxeinx=1という纷换からxが久えてしまうからである。つまり、このような侨瓢簇眶は澄唯泰刨が年眶、すなわち、≈どこにいるんだかさっぱりわからない∽ということである。笨瓢翁が澄年すると疤弥が稍澄年になるという稍澄年拉簇犯が、ここでも悸附している。
悸狠に赂哼する侨瓢簇眶では、いろんな笨瓢翁を积った侨瓢簇眶の脚ね圭わせになっており、笨瓢翁が办つの猛に澄年していない(それ ゆえ嫡にxに簇してはある镍刨は疯まっている)。扦罢の簇眶がフ〖リエ恃垂によってeikxの下の妨にかけるということはすなわち、扦罢の侨瓢簇眶がいろんな笨瓢翁を积った侨瓢簇眶の脚ね圭わせでかならず今けるということである。
n)に疯まっていて、ゆらぎがないということである。
この箕、ψ*ψを纷换すると、xによらない年眶となる。なぜならば、e≥inxeinx=1という纷换からxが久えてしまうからである。つまり、このような侨瓢簇眶は澄唯泰刨が年眶、すなわち、≈どこにいるんだかさっぱりわからない∽ということである。笨瓢翁が澄年すると疤弥が稍澄年になるという稍澄年拉簇犯が、ここでも悸附している。
悸狠に赂哼する侨瓢簇眶では、いろんな笨瓢翁を积った侨瓢簇眶の脚ね圭わせになっており、笨瓢翁が办つの猛に澄年していない(それ ゆえ嫡にxに簇してはある镍刨は疯まっている)。扦罢の簇眶がフ〖リエ恃垂によってeikxの下の妨にかけるということはすなわち、扦罢の侨瓢簇眶がいろんな笨瓢翁を积った侨瓢簇眶の脚ね圭わせでかならず今けるということである。| ㈤ | dx | ψ*(x,t)x |
⑦2 ⑦x2 | ψ(x,t)♂ | ㈤ dx∈ |
⑦2 ⑦x2 | ψ*(x,t) | ) | xψ(x,t) |
| ㈤ | dx | ψ*(x,t) |
⑦2 ⑦x2 | ∈ | xψ(x,t) | ) | =㈤ dx∈ |
⑦2 ⑦x2 | ψ*(x,t) | ) | xψ(x,t) |
| 润陵滦侠弄 |
陵滦侠弄 |
|
| 概诺蜗池 |
ニュ〖トン蜗池 |
陵滦侠弄蜗池∈アインシュタイン∷ |
| 翁灰蜗池 |
シュレ〖ディンガ〖数镍及 |
クラインˇゴルドン数镍及、ディラック数镍及など |