|
| 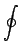 | p dq = nh |
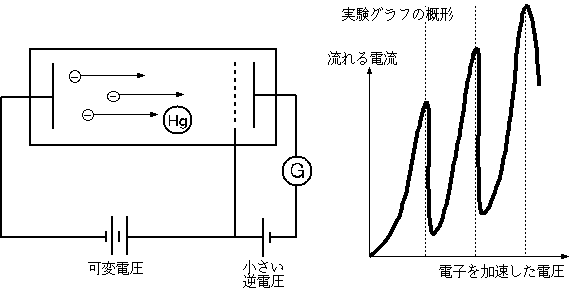 水銀の蒸気を満たした管の中に電子を発生させ、電圧をかけて管内を走らせる。電子がやってき
た先には網と、その後ろに電子を追い返すような逆電圧をかけたプレートが待ち構えている。電圧を高くすれば走ってきた電子は勢いで網を通り抜けてプレート
に入り、検流計に電流が流れるのだが、電圧が4.9Vを超えると、突然電流が減少する。これは管内に放出された電子のエネルギーをもらって、水銀のまわり
を回る電子が励起するからである。この時走ってきた電子はエネルギーを失う。つまり水銀の場合のE2−E1に
相当するエネルギーが4.9eVぐらいであり、4.9eV以下のエネルギーしか持っていない電子では、水銀原子を励起することはできない。ということは逆
に、4.9eV以下のエネルギーしか持っていない電子はエネルギーを取られることはないのである。黒体輻射の話の時も、高い振動数の光が大きいエネルギー
単位(hν)を要求するために逆にエネルギーをもらえない(分配されない)という状況があったが、ここでも同様の現象が起きている。水銀原
子は4.9eV以上というエネルギーを要求するため、それより低いエネルギーを持った電子はエネルギーを奪われることはない(貧乏人は泥棒に狙われな
い!)。電圧が9.8Vを超えると、今度は2個の水銀原子を励起できるので、また電流の減少が起こる(14.7V
でも同様)。この実験によって、原子の回りの電子が確かに基底状態、励起状態という安定状態を持っていることが確認できた。
水銀の蒸気を満たした管の中に電子を発生させ、電圧をかけて管内を走らせる。電子がやってき
た先には網と、その後ろに電子を追い返すような逆電圧をかけたプレートが待ち構えている。電圧を高くすれば走ってきた電子は勢いで網を通り抜けてプレート
に入り、検流計に電流が流れるのだが、電圧が4.9Vを超えると、突然電流が減少する。これは管内に放出された電子のエネルギーをもらって、水銀のまわり
を回る電子が励起するからである。この時走ってきた電子はエネルギーを失う。つまり水銀の場合のE2−E1に
相当するエネルギーが4.9eVぐらいであり、4.9eV以下のエネルギーしか持っていない電子では、水銀原子を励起することはできない。ということは逆
に、4.9eV以下のエネルギーしか持っていない電子はエネルギーを取られることはないのである。黒体輻射の話の時も、高い振動数の光が大きいエネルギー
単位(hν)を要求するために逆にエネルギーをもらえない(分配されない)という状況があったが、ここでも同様の現象が起きている。水銀原
子は4.9eV以上というエネルギーを要求するため、それより低いエネルギーを持った電子はエネルギーを奪われることはない(貧乏人は泥棒に狙われな
い!)。電圧が9.8Vを超えると、今度は2個の水銀原子を励起できるので、また電流の減少が起こる(14.7V
でも同様)。この実験によって、原子の回りの電子が確かに基底状態、励起状態という安定状態を持っていることが確認できた。
| (4.7) |
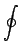 )は周期運動一回分の積分である。2πr ×mv=nhという形だと、円運動にしか適用できないが、この条件なら周期的な運動であればすべて適用できる。
一般化座標qとそれに対応する一般化運動量pの両方を座標として扱った2次元の空間(q,p)(座標がN個あるならば2N次元の空間になる)を位相空間と呼ぶ。時間がたつとqもpも変化していくが、その変化の軌跡は決まった線になる。
ここで、なぜqだけの空間ではなく、pも含めた位相空間を考えなくてはいけないかを説明しておく。運動方程式は
)は周期運動一回分の積分である。2πr ×mv=nhという形だと、円運動にしか適用できないが、この条件なら周期的な運動であればすべて適用できる。
一般化座標qとそれに対応する一般化運動量pの両方を座標として扱った2次元の空間(q,p)(座標がN個あるならば2N次元の空間になる)を位相空間と呼ぶ。時間がたつとqもpも変化していくが、その変化の軌跡は決まった線になる。
ここで、なぜqだけの空間ではなく、pも含めた位相空間を考えなくてはいけないかを説明しておく。運動方程式は
| (4.8) |
|
|
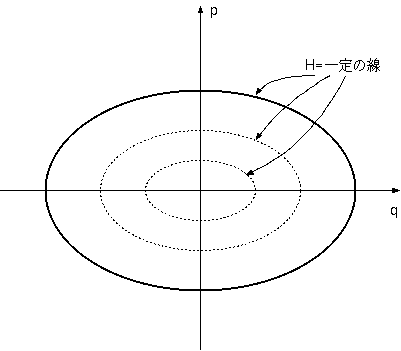
| (4.11) |
|
| (4.14) |
|
| (4.15) |
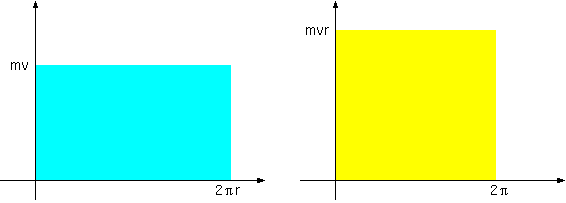 原子模型の場合に話を戻そう。電子が等速円運動しているなら、運動量の大きさはmvで一定で、一周するとq(位置座標)が2πr変化する。これから(4.2) が出る。あるいは、pとして角運動量mvrを取り、対応する座標として角度をとれば、一周は角度2πであるので同じ結果になる。つまり、ゾンマーフェルトの条件はボーアの条件を含んでいる。
原子模型の場合に話を戻そう。電子が等速円運動しているなら、運動量の大きさはmvで一定で、一周するとq(位置座標)が2πr変化する。これから(4.2) が出る。あるいは、pとして角運動量mvrを取り、対応する座標として角度をとれば、一周は角度2πであるので同じ結果になる。つまり、ゾンマーフェルトの条件はボーアの条件を含んでいる。
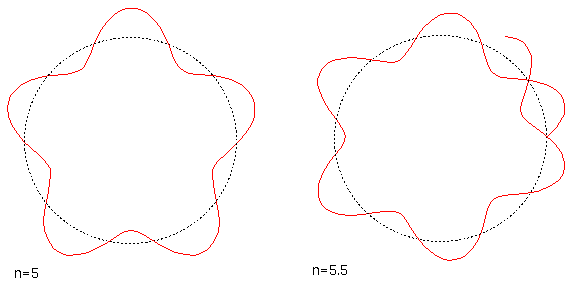
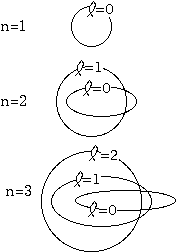 楕円運動(に相当するもの)を含めた詳しい計算は後で、より物質の波動性との関連が明らかになってから行うが、簡単に結果を述べておくと、やはりこの場合も量子条件により、どんな形の楕円でもいい、というわけにはいかない。許される電子の軌道は主量子数と呼ばれるn(自然数)と、軌道量子数と呼ばれるl(0以上の整数で、最大値はn−1。楕円の扁平さを表す)、および磁気量子数と呼ばれるm(整数で−l < m < l。軌道の傾きを表す。±lの時もっともz軸周りの角運動量が大きい)で分類できる。エネルギーは主量子数nだけに依存する(E=−[(E1)/(n2)])。主量子数nの状態には、l = 0,1,2,…,n−1の状態27 があり、各々のlの値に対し磁気量子数が−l からlまでの2l+1 個ずつある。よって主量子数nの状態は
楕円運動(に相当するもの)を含めた詳しい計算は後で、より物質の波動性との関連が明らかになってから行うが、簡単に結果を述べておくと、やはりこの場合も量子条件により、どんな形の楕円でもいい、というわけにはいかない。許される電子の軌道は主量子数と呼ばれるn(自然数)と、軌道量子数と呼ばれるl(0以上の整数で、最大値はn−1。楕円の扁平さを表す)、および磁気量子数と呼ばれるm(整数で−l < m < l。軌道の傾きを表す。±lの時もっともz軸周りの角運動量が大きい)で分類できる。エネルギーは主量子数nだけに依存する(E=−[(E1)/(n2)])。主量子数nの状態には、l = 0,1,2,…,n−1の状態27 があり、各々のlの値に対し磁気量子数が−l からlまでの2l+1 個ずつある。よって主量子数nの状態は
| (4.16) |
| (5.1) |
| (5.2) |
| (5.3) |
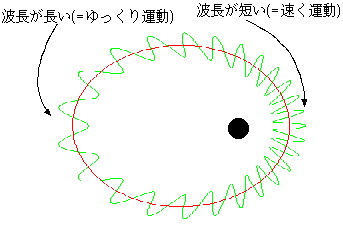 古典力学的に考えると「位置エネルギーVが増えると運動エネルギーが減る」という現象が起きているが、波動として考えると「Vが大きい場所では波長が伸びる」という現象が起きていることになる。ド・ブロイの波動力学では、位置エネルギーというものへの捉え方が古典力学とは違ってきている。結果としてこの二つの力学が同じような結果を示すようになっているのである(詳細は後で示す)。
なお、このような図を見て「電子が外へ内へと振動している」というふうに勘違いする人がよくいるので念のため注意しておくが、
古典力学的に考えると「位置エネルギーVが増えると運動エネルギーが減る」という現象が起きているが、波動として考えると「Vが大きい場所では波長が伸びる」という現象が起きていることになる。ド・ブロイの波動力学では、位置エネルギーというものへの捉え方が古典力学とは違ってきている。結果としてこの二つの力学が同じような結果を示すようになっているのである(詳細は後で示す)。
なお、このような図を見て「電子が外へ内へと振動している」というふうに勘違いする人がよくいるので念のため注意しておくが、
絵で外へ内へと振動しているように描かれているが、それはあくまで図を描く都合上であって、物質波は方向のない波(スカラー波)である。後で波動関数という形でこの波を表現するが、その波動関数にも方向はない29。ではいったい何の波なのかということについては、後で述べる。物質波には方向はない。