
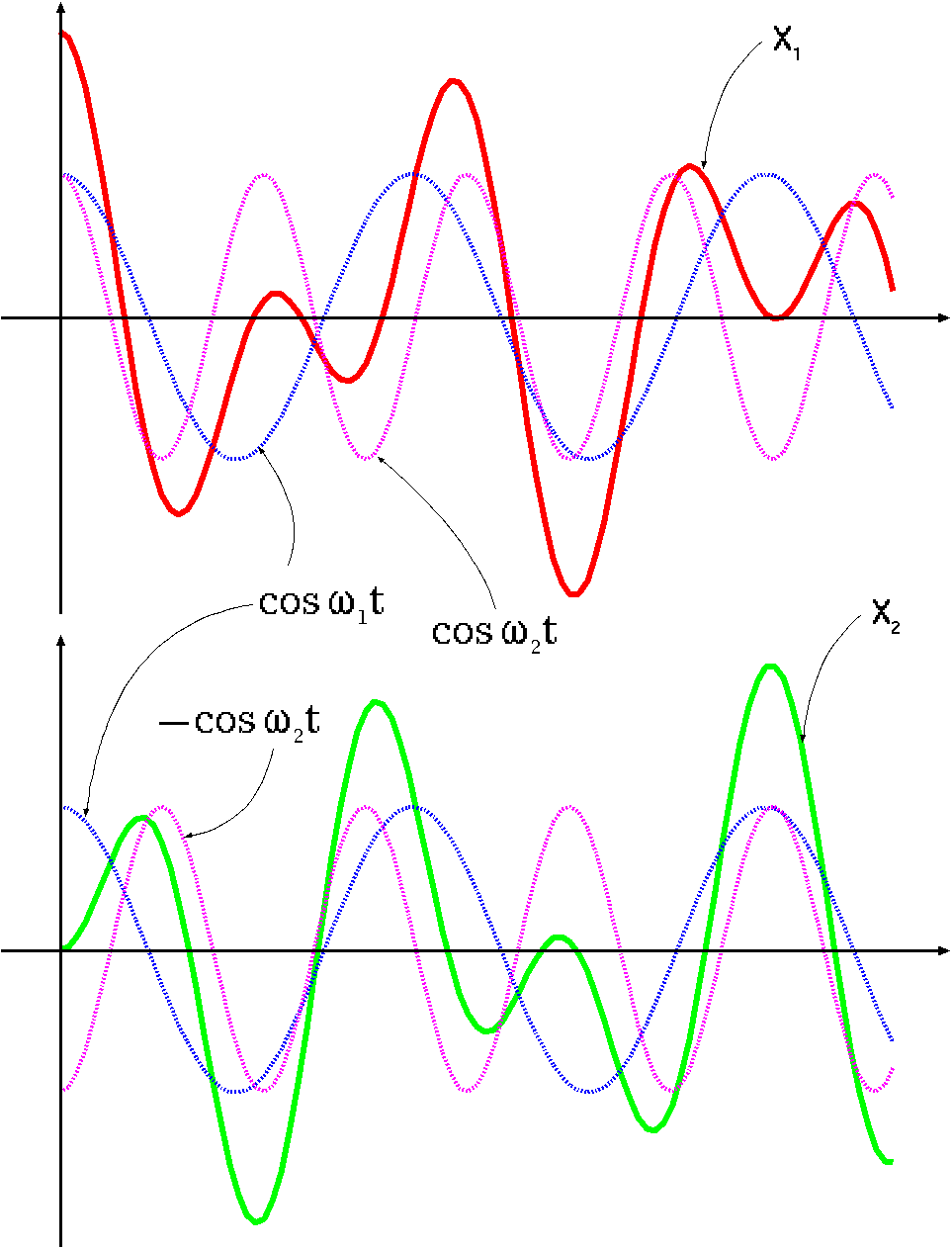
 C1=C2=A/2とした場合の解(実数部を取った)
C1=C2=A/2とした場合の解(実数部を取った)
|
|
|
|
|
(3.18) |
|
(3.19) |
|
(3.20) |
|
(3.21) |
|
(3.22) |
|
|
(3.25) |
| ( |
|
) |
| ( |
|
) |
| ( |
|
) |
| (何か)×( |
|
) |
|
(3.26) |
| |
|
( |
|
) |
|
(3.27) |
| ( |
|
) |
|
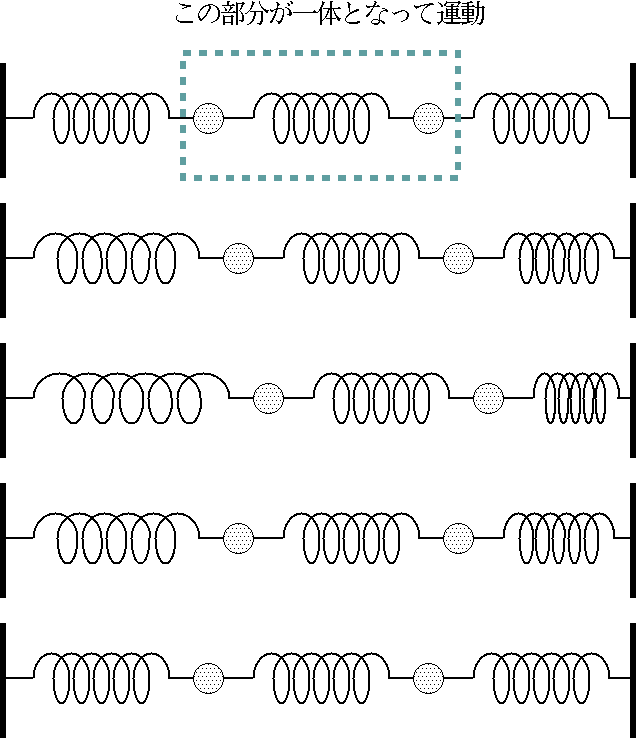
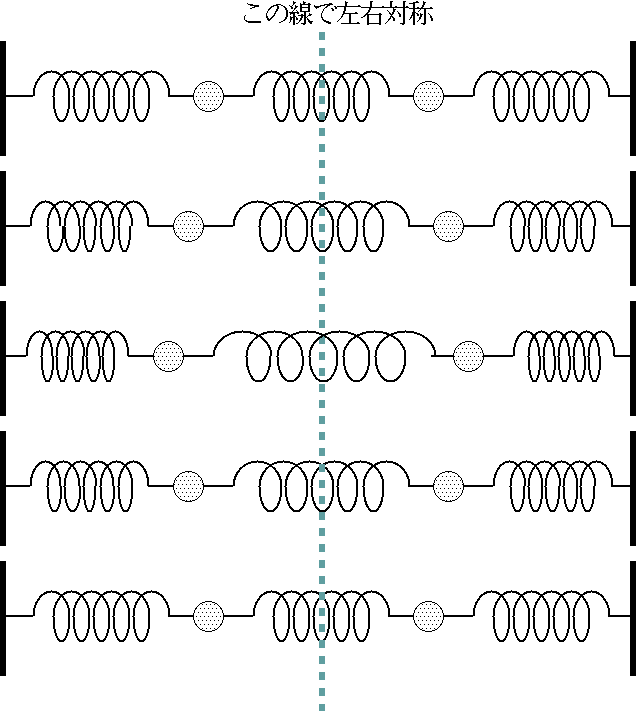
固有ベクトルと固有値
ベクトルにある行列Mをかけた時、結果が元のベクトルに比例するベクトルになる時、そのベクトルをMの「固有ベクト
ル(eigenvector)」
と呼び、この時出てくる値λを「固有値(eigenvalue)」と呼ぶ。N×N行列の場合、固有値は最大N個ある。
対称でない行列の時は行列をどっちから書けるかによって、
と区別するが、いまMは対称行列なのでこの区別はない。 これはつまり、「固有ベクトルがかけられるとわかった時は、行列を単なる 数(固有値)に置き直してもよい」ということになる。つまり複雑な行列を固有値という「ただの数」に変更することができる。これが固有ベクトルを使うと計 算が楽になる理由である。 |
| ( |
|
) |
|
(3.29) |
| ( |
|
|
) |
|
(3.30) |
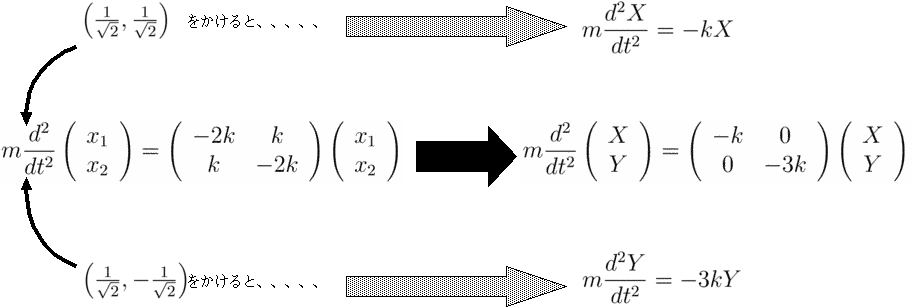
|
(3.31) |
| ( |
|
|
) |
| ( |
|
|
) |
|
(3.32) |
|
(3.33) |
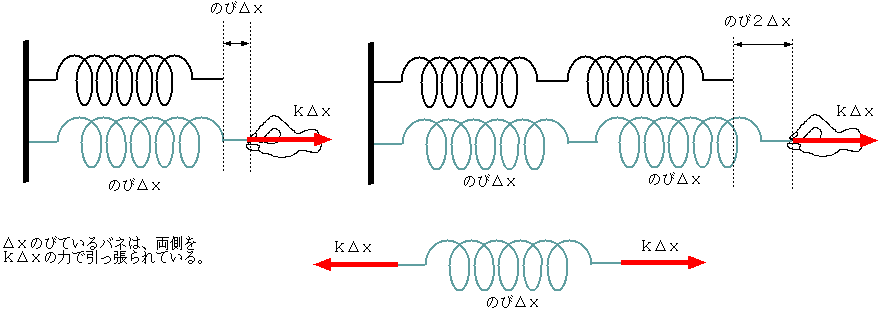
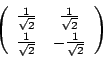 は
は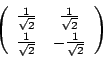 の逆行列だからである(このように「逆演
算」を「逆行列」で計算できるのも行列の強み)。
以上で行った計算をもう一度見直そう。元々の運動方程式(3.25)に行列
の逆行列だからである(このように「逆演
算」を「逆行列」で計算できるのも行列の強み)。
以上で行った計算をもう一度見直そう。元々の運動方程式(3.25)に行列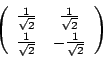 をかけると、左辺
は(X,Y)の式になる。右辺にも(3.33)を代入して、
をかけると、左辺
は(X,Y)の式になる。右辺にも(3.33)を代入して、
|
(3.34) |
|
(3.35) |
| ( |
|
) |
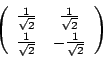 という行列と、その逆行列であるT−1(た
またま、今の場合はTと一致した)ではさんで、 T−1M
Tという行列を計算し、
という行列と、その逆行列であるT−1(た
またま、今の場合はTと一致した)ではさんで、 T−1M
Tという行列を計算し、
| ( |
|
|
) |
|
(3.36) |
| ( |
|
) |
|
(3.37) |
|
(3.38) |
|
(3.39) |
|
(3.40) |
|
(3.41) |
| ( |
|
) |
|
(3.42) |
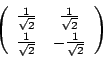 の逆行列が自分自身になったのは偶然ですか?
の逆行列が自分自身になったのは偶然ですか?