|
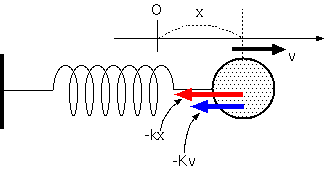 ばね振り子を考える。ただし、いつも前提として置く「空気の抵抗を無視して」を今回はとっぱらって、空気の抵抗をちゃんと計算にいれてみよう。空気の抵抗
がどんな式になるかはいろんな考え方があるが、ここでは速度[dx/dt]に比例するとしよう。その比例定数をKで表すと、運動方程式は
ばね振り子を考える。ただし、いつも前提として置く「空気の抵抗を無視して」を今回はとっぱらって、空気の抵抗をちゃんと計算にいれてみよう。空気の抵抗
がどんな式になるかはいろんな考え方があるが、ここでは速度[dx/dt]に比例するとしよう。その比例定数をKで表すと、運動方程式は
|
(2.1) |
|
(2.2) |
|
(2.3) |
|
(2.4) |
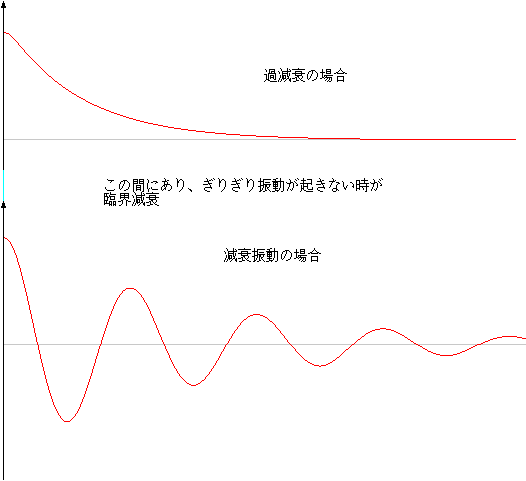
| [K2−4mk > 0の時] |
|
(2.5) |
| K2−4mk < 0の時 |
|
(2.6) |
|
(2.7) |
| K2−4mk=0の時 |
|
(2.8) |
|
(2.9) |
| ( | d
dt |
+ | K
2m |
) | X= e−[K/2m]t |
|
(2.10) |
|
(2.11) |
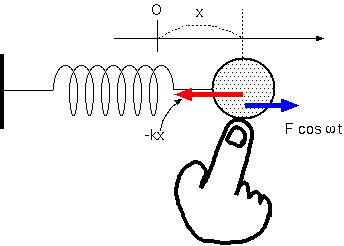 前節は抵抗が働く場合(つまりエネルギーがロスする場合)であったが、今度は逆にエネルギーが外部から注ぎ込まれる場合(つまり、外部から力を加えて振動
を起こさせる場合)を考えよう。
前節は抵抗が働く場合(つまりエネルギーがロスする場合)であったが、今度は逆にエネルギーが外部から注ぎ込まれる場合(つまり、外部から力を加えて振動
を起こさせる場合)を考えよう。
|
(2.12) |
|
(2.13) |
|
(2.14) |
|
(2.15) |
|
(2.16) |
|
(2.17) |
|
(2.18) |
|
(2.19) |
|
(2.20) |
|
(2.21) |
|
(2.22) |
|
(2.23) |
| ( | d
dt |
+ | K
2m |
) | te−[K/2m]t |
| d
dt |
(te−[K/2m]t
) |
| K
2m |
|
te−[K/2m]t |
| K
2m |
|
te−[K/2m]t |